大工さんはイデアのエージェントである
＜PS理論との共振：道元禅をカテリーナ曲線で示すとどうなる＞の続き
http://www.beach.jp/circleboard/ad00178/topic/1100200464613

悟の原理は微小の構造を明らかにすることだといいました。禅に限らず真善美のすべてに微小の構造と方向が存在するでしょう。すべては微小から始まるのですね。真善美のすべてについて探求する余裕がありませんので真理と美について絞って行きましょう。

日本の美に対する感性が表現されているのが神社仏閣の建築だと思うのです。それと真理がどう関係しているのでしょうか？

そこで屋根のアーチの形に着目してみます。屋根には美があります。その美を演出しているのがイデアのエージェントである大工さんです。大工さんの美の術を例にとってイデアエージェント説（数学を駆使してイデアを美として表現する）を証明してみることにしましょう。

大工さんがやっていることは鎖を垂らして釣り合うところを探すということです。それが最も端的に現れるのが中心線ですね。その中心線は高さyであり、横は中心から手で摘まんでいるとことまでの距離xです。ここに大きな三角形がありますね。

三角形の辺の長さsはピタゴラスの定理を使うとs^2=x^2+y^2ですね。いくら何でもこのsを垂れ下がった曲線と同じと看做すことはできませんね。誤差が大きすぎるからです。s^2=x^2+y^2は微小構造ではないということです。微分を使うためには微小構造を明らかにすることがすべてなのです。

そこで、中心より最も右、つまり、手で摘まんでいる場所に近づいてみましょう。限りなく近づいたかところで三角形を作ります。これならどうでしょうか？

イメージとしては◤ですね。大きくても小さくても位相的には同じですが、微小にすると意味が違ってきます。限りなく微小（0に近い）なら辺の長さと曲線を近似できそうですね。あくまで仮想の近似です。悟りを得るのに中庸を維持するなら悟りを保証するという宣言（定理）がありましたがこれがそうですね。現在の意識状態が中庸（苦でもなく楽でもない）なら微小な仮想の未来でもその意識が持続しているでしょう。その意識を積分すれば空になるという論理ですね。限りなく微小（0に近い）のですから現在の意識と未来の意識が同じと言うのは当たり前のことですね。

しかし、心はころころ変わるのが現実ですね。明日の心と今日の心が同じだとは決して言えないのですよね。ところが、限りなく微小（0に近い）なら保証できるのですから、それを延長しても保証できるというのですね。まさにトリックですね。仏教では嘘も方便と言いますのでトリックでも何でも悟りが得られるなら由としましょう。

マクロではs^2=x^2+y^2が成り立ちますが、これを曲線と看做すことはできません。そこで曲線を直線と看做す微分を使うのですね。

微分法
http://ms-laboratory.jp/zai/bas2/index.htm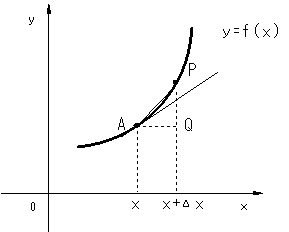


微分の定義はf'={f(x+Δx)-f(x)}/Δx:（limΔx→０）ですから曲線APを接線＝直線と看做しているのですね。確かにΔxを限りなく0に近づけるとAP=接線になりますね。上の図ではAP^2=AQ^2+QP^2が微小構造ですね。このAPを微小部分の辺の長さ（接線）をds、Δxをdx、QPをdyとするとds^2=dx^2+dy^2となりますね。

後はこの微小部分dsを足すと全体の鎖の長さlとなりますね。曲線が直線になってしまいましたね。これはトリックなのですが文句のつけようはないでしょう。

今求めたいのは最小になるポテンシャルエネルギーUですので、全体としてはｌにmgy（質量・重力・高さ）を掛けたU=mgylとなります。mgは分かっていますのでyとlが分かれれば求まります。問題はyとlが分かっていないことです。高さは場所によってまちまちですし、長さは微小部分を足しこまなければなりません。このような場合に力を発揮するのが微分法なのですね。微分は認識方法であると言いましたがアリの認識法であると言ったほうが適切でしょう。

微分積分は認識法である
http://www.beach.jp/circleboard/ad00178/topic/1100200455023

微小部分のポテンシャルエネルギーはmgydsですので、全体のポテンシャルUは

U=∫mgyds（ただし、積範囲は鎖の両端）

となるでしょう。一方、ピタゴラスの定理から

ds^2= dx^2+dy^2

ですので、これを変形すると

ds^2=｛(dx^2+dy^2)/dx^2）｝dx^2=(1+ dy^2/dx^2)dx^2

dy^2/dx^2=y'^2とすると、

ds=√(1+y'^2)dx

となります。従ってmgydsはmgy√(1+y'^2)dxとなり、U=∫mgydsを整理すると、

U=mg∫y√(1+y'^2)dx

となるでしょう。

最小作用を求める式は

I=∫fdtですから、I=U、f=y√(1+y'^2)とすると

I=mg∫y√(1+y'^2)dx

の最小値を求める問題へと収斂します。fがyとy'の変数になっていることがこの式展開のポイントですね。

これは、結局、オイラー方程式

Әf/Әy-d/dx(Әf/Әy')=0

のfをy√(1+y'^2)として「解け」ということです。

オイラーの式というのは最小作用を求める過程で未知の力を想定しておいて、具体的な問題が現れた時に、関数を探し出して当てはめるというトリックを使うのですね。これが何にでも当てはまるというのですがから不思議なことです。結論だけを言いますと、

Әf/Әy-d/dx(Әf/Әy')=y/√(1+y'^2)＝一定

となり、これを積分すると、

y=C1coshC2x

となります。この導出過程はかなり込み入っていますのでこちららを参照してください。

懸垂線
http://analytical-mechanics.matrix.jp/catenary.html

これが双曲線関数(ハイパーボリックコサイン)と呼ばれる曲線です。如何でしょう。大工さんが双曲線の形を作るときこんな面倒な計算を無意識に頭の中でやっているのでしょうか？

とても信じられませんが、少なくとも、これと同等なアルゴリズムがなければ、美の形は偶然には実現しないということですね。

今回は、ラグランジュの方程式ではなくオイラーの方程式を使いましたが、その違いが人称認識と関係するのでそれについては別途に探求します。